The Internet has clearly changed the insurance business. Customers have more choices and increased sensitivity to price, leading to price pressure. Insurers can gather competitor quotes online and analyse them to understand the entire competitive market and their position within that market. However, acquiring competitor quotes and analysing them in an efficient manner is a challenge which is new to most insurers.
Traditionally, pricing actuaries spend a major part of their time analysing historical data. A precise estimate of the cost of a policy remains the foundation for profitability, which is why risk modelling is a core task of any pricing team. During this process, actuaries produce a variety of graphs and statistics, prepare their data in different ways, evaluate interactions1 between variables, analyse the added value of third-party data and examine trends in the data.
Once an actuarial best estimate for the price of a policy has been derived (and loadings for expenses and margins are added), the question arises whether this is the price the company wants to quote. The answer depends on many factors, such as whether it is an existing customer or a new customer, the distribution channel through which the product is offered, the strength of the brand of the insurer, the price sensitivity of the customer and the number of competitors on the market and their prices.
For insurance companies to be able to compete, it is crucial to have an understanding of their competitors’ tariffs. Machine learning techniques are an excellent tool set for this problem.
Beyond an actuarial best estimate premium
On price comparison websites (also known as “aggregators”), all offers may be compared on a single web page. But competitor prices are not only of interest for online business but also for business written by tied agents. It is not uncommon for customers to walk into an agency with a competitor quote. Agents are better prepared for discussions with clients if they already know the main competitor is likely to have a lower quote for the given customer.
From the perspective of a customer, especially a price-sensitive one, aggregators provide an ideal platform. Customers can compare all competing offerings by only providing their details once. Of course, not all market players might actually be present on this platform (or at least not all product offerings), and certainly the coverages of the different offerings will not be identical. But these two aspects are either negligible to many consumers or they do not even know about them.
Making the most out of the available information
Many insurers analyse their competitive positions for certain customer segments (e.g., young female drivers with inexpensive cars in a certain region) and use this information when updating the tariffs of their own products. Some insurers still pursue ways of obtaining competitor prices beyond aggregators, such as web scraping, outsourcing or mystery shopping, a cumbersome and expensive market research tactic where people are sent “undercover” to retrieve consumer information. Others, however, go a step further and try to reverse engineer competitor tariffs. This means that they try to find out the pricing formula and the different loadings their competitors are using.
However, reverse engineering a competitor tariff without complete knowledge about the tariff structure is a very difficult task in general. Consider a European motor insurance tariff. Often, a multiplicative tariff structure based on a generalised linear model (GLM) is used. Thus one approach to reverse engineer a tariff is simply to assume a certain tariff structure and to derive the relativities2 using the competitor data gathered. What sounds reasonably simple is not so straightforward because:
- It is not known which variables are used in the tariff.
- The groupings3 for the variables are unknown.
- It is not known which interactions are used by the tariff.
- The tariff might use third-party data, such as sociodemographic data or data on creditworthiness. Some of this data might not be publicly available.
- The vehicle grouping4 may be unknown.
- The tariff might consist of multiple additive and multiplicative elements such as expense loadings or a certain basis premium.
- The premium may only be available at an aggregated level. A liability premium may, for instance, consist of one premium formula for attritional losses and one for large losses. These two premium elements could be the product of different relativities, which is not apparent from the outside.
- The tariff structure might not be multiplicative. The underlying model may not even be a GLM but a model based on an entirely different statistical concept.
In many instances, it is virtually impossible to find the exact formula used by a competitor because there are simply too many possibilities to be evaluated and compared, even in cases where only a selection of the above issues can occur.
Enter machine learning
Machine learning is a computer science discipline focused on algorithms that learn from data as they go. Such algorithms make many fewer assumptions about the data structure than other modelling concepts and can, therefore, be applied to a variety of problems. Also, they are more automated because there are fewer input parameters needed, which speeds up the model-building process. In the insurance sector, machine learning algorithms are used for various tasks such as detecting fraud, pricing and processing telematics data.
We examined the results of an analysis where we used machine learning to derive an estimate for a motor insurance premium. We gathered 20,000 quotes from a website to build this model. The premium we modelled was the sum of three different elements: liability, own damage (partial casco) and collisions. It is extremely likely that these three premium elements have their own underlying tariff structures (as it is market practice). Still, for this case study, we decided to model the three premium elements as a whole. We note that we had no knowledge of the underlying tariff structure. For instance, we did not know which rating variables were used by the tariff and therefore simply fed our model with all available variables we possessed. The variables which were used for this were the same variables which an insurer would use to derive the pricing of a policy: data of the policyholder (age, gender, place of residence, license date), information on the insured car (make, model, price) and so forth. We used a combination of multiple decision tree models, a so-called ensemble, to model the premium. The algorithm is driven by the data: it uncovers patterns and follows them to model the premium as best as it can. This shows the flexibility which machine learning algorithms can provide.
Figure 1 shows the absolute value of the relative error on validation data, i.e., data which was not used to build the model. We can, for instance, see that for 50% of the validation data, our estimated premium was within 3.2% of the true competitor premium. Similarly we can see that the relative error is less than 10% for about 95% of the data. In fact, only 0.7% of the validation data has an error larger than 20%. The average absolute relative error was at 4%.
Figure 1: Competitor Premium Estimation Error on Unseen Validation Data
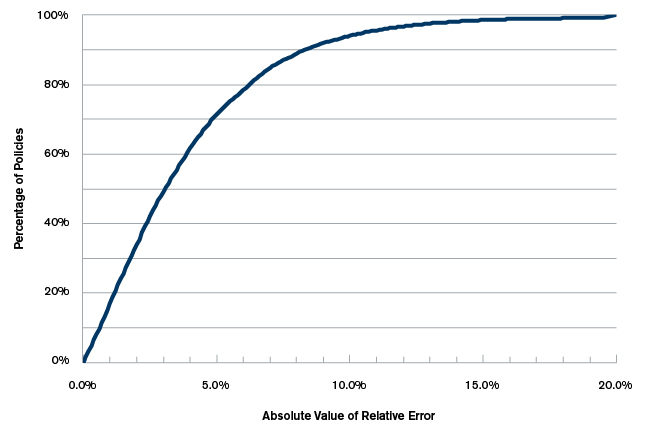
In a market where a competitor premium can easily be 10%, 20% or even 30% lower or higher than one’s own premium (which is not at all uncommon), an estimation error of 4% seems quite good. Still, one might say that this is not accurate enough. In this case, there are two straightforward ways to improve the accuracy of the model:
1. Build three different models for the three individual premium elements.
2. Gather more data to train the algorithm.
By producing a model for each individual coverage, we provide the algorithm with a more robust target. If we feed the model with more data, it will be able to model more granular effects, which will improve the performance of the model. Also, if we have any a priori knowledge about the tariff, we can use that, too. We may, for instance, know the grouping of certain variables (maybe the region or vehicle classes) or we may even know the exact relativities for one variable (possibly from the advertisement of a discount). Such information can be used to pre-process the data which is fed into the machine learning algorithms, which will reduce the degrees of freedom and improve the estimation error.
The flexibility of machine learning algorithms also enables us to model, for instance, the premium of the third-lowest offering. Of course, one would need the appropriate data. In this case, that would be the quote which ranks third for a sizeable sample. We note that, compared with modelling the premium of a single competitor, it will be more difficult to model the premium of the third rank. Such a model would effectively depend on the tariffs of all market players as different competitors with different tariffs will rank third, depending on the profile quoted. But the results of such a model can provide valuable insight. It would allow an insurer to adjust its own tariff (probably only for certain customer segments) such that it ranks third or less. Similarly, one could target a position within the top 10 for each policy.
Better informed decisions
Machine learning techniques provide a flexible tool set to derive accurate estimates of competitor premiums without any knowledge about the underlying tariff structure. The machine learning approach we developed as part of our research is faster and much less expensive than exhaustive web scraping or mystery shopping. It has enabled insurance executives to make better informed decisions about not only tariff changes, but also marketing campaigns and commercial discounts for certain customer segments. The impact of a tariff change on profitability and business volume can certainly be much better assessed in the presence of competitor premiums. In an ideal scenario, a company has an estimate of the competitor premiums at the point of sale. This allows adjusting one’s own quote to increase either the probability of conversion (by lowering the quote) or the profitability (by increasing the quote).
1The term "interaction" refers to the fact that the loadings depend on the attributes of more than one variable. For instance, a 23-year-old married driver might have to pay 3% less than a 23-year-old unmarried driver. But if the two drivers are both age 40, the discount for the married driver might be only 1%. In this case, we have an interaction between marital status and policyholder age.
2With the term "relativity," we refer to the relative loading for a given risk detail. For instance, the relativity for house owners could be 97% and for owners of a flat 98%, compared with 100% for tenants. In this case, a house owner would pay 3% less for motor insurance than a tenant (assuming all other policy details are the same).
3For more robustness, the different values of rating factors are often aggregated into groups. For instance, an age variable might be grouped like this: 18, 19, 20, 22-23, 24-25, 26-30, 31-35, 36-40, etc. In this case, a person aged 36 will have the same premium as someone aged 40.
4Many insurers group cars into so-called vehicle groups, where cars in the same vehicle group will have the same premium. The vehicle group generally depends on the car’s properties (such as power, weight, price, brand, number of seats, type of car, etc.). In many instances, every company has its own vehicle groupings, but there are also markets (such as Germany) where an industry grouping is used.